« Notre passé fait partie de notre culture présente, et nous pouvons légitimement l’y intégrer ; mais nos connaissances présentes ne font pas partie des cultures passées, et nous ne devons pas les présupposer acquises quand nous faisons de l’histoire – qu’il s’agisse d’histoire des sciences, d’histoire de la philosophie ou de toute autre. », Gérard Simon, Sciences et Savoirs aux XVIe et XVIIe siècles, 1996, p 28.
De l’Antiquité grecque à Alhazen et à Kepler
Notre connaissance de l’optique au temps de l’Antiquité grecque repose essentiellement sur deux ouvrages écrits à plus de cinq siècles d’intervalle. Le premier est le traité d’optique d’Euclide, célèbre mathématicien qui vécut vers le IVe siècle avant notre ère. On ne connaît quasiment rien de sa vie, mais son Optique nous est parvenue intégralement en grec.
Le second est l’Optique de l’astronome Ptolémée qui vécut à Alexandrie au IIe siècle. Si son grand traité d’astronomie est bien connu grâce aux traductions qu’en ont faites les savants arabes à partir VIIIe siècle sous le titre d’Almageste1, une partie seulement de son traité d’optique nous est parvenue2.
 |
 |
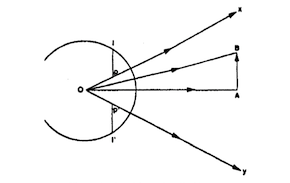
Ptolémée reprend et développe l’analyse mathématique d’Euclide. Parmi les différentes théories de la vision développées par ses prédécesseurs – théories qui en l’absence de preuves sont nécessairement fondées sur des spéculations –, il opte comme Euclide en faveur de celle reposant sur la notion de rayon visuel « émané de notre œil et allant frapper l’objet »3.
Si cette théorie s’avérera fausse – le rayon visuel ne sort pas de l’œil mais y pénètre –, elle n’empêche pas d’avoir une connaissance juste de certains phénomènes optiques, et notamment de ceux qui peuvent être interprétés de façon purement géométrique : réflexion sur un miroir plan et réfraction d’un milieu à un autre (de l’air dans l’eau ou de l’air dans le verre par exemple).
Comme Euclide, Ptolémée connaît donc la loi régissant le rayon visuel réfléchi. En ce qui concerne le rayon visuel brisé (réfraction), il réussit à produire expérimentalement quelques tables de déviation, mais ne parvient pas à établir la loi des sinus qui régit ce phénomène. Ptolémée est aussi le premier astronome – et bien sûr pas le dernier – à s’intéresser à la réfraction atmosphérique qui affecte ses observations de la Lune et du Soleil.
Malgré ces avancées notables dans le domaine de phénomènes optiques –particulièrement importants pour le développement ultérieur de l’astronomie de position (réfraction atmosphérique) et de l’astronomie instrumentale (réflexion sur un miroir, réfraction de l’air dans le verre)– la théorie de la vision de Ptolémée l’empêche de développer une science optique cohérente. Comme dans sa théorie purement géométrique l’œil n’a d’autre rôle que celui d’émetteur du rayon visuel, Ptolémée n’est pas amené à s’interroger sur le fonctionnement de cet organe. Or en l’absence de questionnements sur ce qui pénètre dans l’œil – la lumière – et sur l’image formée dans et par l’œil, la théorie optique ne peut progresser.
En s’appuyant sur le concept de rayon visuel issu de l’œil, il ne s’interroge ni sur la lumière qui pénètre dans l’œil, ni sur le statut de la formation de l’image perçue.
La vision selon Ptolémée (cliquez sur l’image pour agrandir)
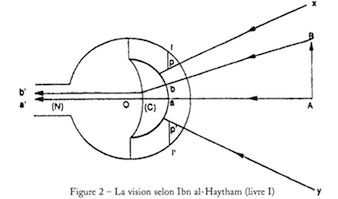
Huit siècles environ après Ptolémée, le savant arabe Ibn al-Haytham4 connu sous le nom d’Alhazen dans l’Occident médiéval – s’intéresse de façon très novatrice aux questions d’optique et de vision. Il est en effet le premier à les aborder en procédant à des expériences. Nombreuses et reproductibles, celles-ci vont l’amener à apporter la démonstration que « la vision se produit grâce à des rayons lumineux qui pénètrent dans l’œil et non grâce à des rayons visuels qui en sortent, comme le postulait l’optique géométrique de l’Antiquité »5.
Les travaux d’Alhazen permettent donc de trancher définitivement entre les différentes théories spéculatives de la vision qui étaient en concurrence depuis l’Antiquité grecque. En inversant le sens des rayons visuels, Alhazen soulève en outre la question de la formation des images, question restée sans objet tant que le rayon visuel était supposé sortir de l’œil pour aller palper directement l’objet vu.
La vision selon Alhazen (cliquez sur l’image pour agrandir)
Diffusée dès le XIIe siècle en Occident et rapidement adoptée, la conception véritablement révolutionnaire de la vision établie par Alhazen suscite des travaux à la fois sur la nature de la lumière et sur le fonctionnement de l’œil – organe de la formation de l’image.
*
Au tout début du XVIe siècle la théorie de l’intromission des rayons visuels est reprise et améliorée par l’astronome allemand Kepler, savant autant intéressé par la théorie que par la pratique.
En étudiant les observations de Mars que lui a léguées à Prague Tycho Brahé – son illustre prédécesseur danois à la cour de l’empereur Rodolphe II –, Kepler est amené à s’intéresser aux corrections de réfraction atmosphérique, et plus généralement aux phénomènes optiques.
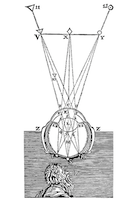
Dans le même temps Kepler étudie le phénomène de la vision – y compris dans sa dimension physiologique. En 1604, il est le premier à établir que l’œil fonctionne comme une chambre noire.
Illustration extraite de "La Dioptrique" de Descartes montrant la formation de l’image sur la rétine
(dans son ouvrage "Astronomia Pars Optica" publié en 1604 Kepler n’a pas inclus d’illustration de sa théorie de la vision).
En 1610, le duc de Bavière est de passage à Prague et prête pendant quelques mois à Kepler une lunette construite selon le modèle mis au point à Venise l’année précédente par Galilée.
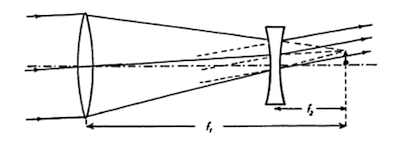
Peu après, Kepler en établit la théorie, ce que Galilée n’avait pas fait, et s’empresse d’en concevoir une amélioration radicale. Comme Galilée, il place à l’avant du tube de sa lunette une lentille en verre convergente qui produit une image de l’astre. Mais, tandis que pour grossir cette image Galilée place à l’arrière du tube un oculaire divergent, Kepler utilise un oculaire convergent.
 |
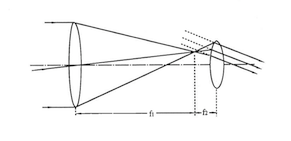 |
| La lunette de Galilée (cliquez sur l’image pour agrandir) | La lunette de Kepler (cliquez sur l’image pour agrandir) |
Dans le même temps Kepler établit la toute première théorie des lentilles – qu’il publie en 1611 dans son ouvrage Dioptricae.
Du telescopium à réfraction au telescopium à réflexion
Curieusement, l’instrument grâce auquel Galilée a réalisé depuis 1609 ses grandes découvertes est resté sans nom. C’est grâce au prince Cesi qu’en avril 1611 il est baptisé telescopium. Fondateur en 1603 de l’Académie des Lynx, première académie savante européenne, Cesi invente cette dénomination à l’occasion d’un repas organisé par les membres de son académie en l’honneur de Galilée.
Cependant, peu pratique pour les astronomes, le telescopium de Galilée tombe rapidement dans l’oubli. Contrairement au telescopium de Kepler dont l’usage se répand dans toute l’Europe et que les Allemands appelleront Fernrohr ou Refraktor, les Anglais (refracting) telescope, les Français lunette astronomique et les Italiens telescopio.
Vers 1668, le jeune savant anglais Newton s’intéresse à un phénomène optique mystérieux : l’ « apparition » (en latin spectrum) de lumières colorées après qu’un faisceau de lumière blanche a traversé un prisme de verre. Il effectue de nombreuses expériences pour tenter de comprendre comment se produit cette décomposition de la lumière blanche. L’une d’elles – qui consiste à envoyer un faisceau de lumières colorées sur une lentille puis sur un prisme de verre – permet à Newton de recomposer en lumière blanche des lumières colorées… et de démontrer que l’apparition (spectre) des couleurs provient non des qualités intrinsèques du verre mais de la lumière blanche elle-même.
Newton établit ensuite que les différentes couleurs cachées dans la lumière blanche ne sont pas toutes déviées du même angle en traversant un prisme. Ce qui l’amène à établir les lois de la réfraction.
Grâce à ces outils théoriques, Newton réussit à expliquer pourquoi l’image d’un astre observé à l’aide d’une lunette de Kepler est colorée : après réfraction à travers une lentille, la couleur violette converge plus près de la lentille que la couleur rouge, de sorte que lorsque l’on observe l’image de l’astre avec l’oculaire elle présente un aspect irisé.
Cette aberration chromatique est d’autant plus gênante que le foyer de la lentille est court. Ce qui au fil du temps a conduit les astronomes à construire des lunettes de plus en plus longues – bien peu pratiques à manipuler.

Lunette aérienne de 66 m de long. Gravure extraite de l’ouvrage de Huygens
"Astroscopia Compendiaria tubi optici molimine liberata" publié en 1684.
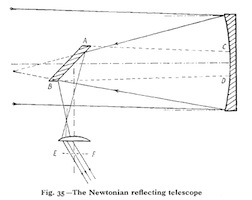
Convaincu – à tort – que ce défaut du telescopium de Kepler est rédhibitoire, Newton invente un nouvel instrument exempt d’aberration chromatique. Son telescopium forme l’image de l’astre non par réfraction à travers une lentille convergente, mais par réflexion sur un miroir concave. Puisque toutes les couleurs de la lumière blanche convergent en un même point après réflexion sur un miroir, l’image produite par le télescope à miroir est bien exempte de l’aberration chromatique dont souffre l’instrument de Kepler.
Lorsqu’en 1668 Newton construit un premier prototype de son telescopium à réflexion, il polit un miroir concave de quelques centimètres de diamètre qu’il a lui-même fabriqué avec un alliage métallique hautement réfléchissant de sa composition.
Le télescope de Newton (cliquez sur les images pour agrandir)
Intéressée par cette invention, en 1671 la Royal Society prie le célèbre mathématicien de Cambridge de lui présenter son invention. L’année suivante le nouvel instrument fait l’objet d’une vive controverse. Newton ne serait pas le précurseur qu’il prétend être car dès 1663 un brillant mathématicien écossais, Gregory, a publié dans son ouvrage Optica promota la description d’un telescopium à miroir concave.
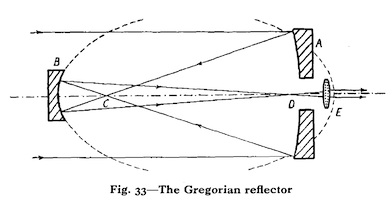
Le télescope de Gregory (cliquez sur l’image pour agrandir)
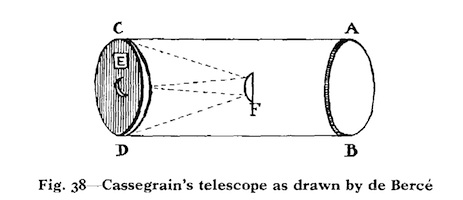
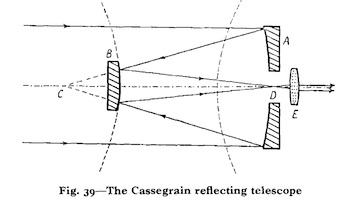
Qui plus est, peu après la publication en 1672 dans le Journal des Sçavants d’une présentation louangeuse du télescope de Newton par Huygens, paraît dans le même journal la description d’un troisième télescope à miroir, dû celui-là à Cassegrain, obscur professeur au collège royal de Chartres.
Le télescope de Cassegrain (cliquez sur les images pour agrandir)
De la théorie à la pratique
Gregory et Cassegrain ont tous deux imaginé l’astronome observant à l’arrière de l’instrument – comme dans le cas de la lunette de Kepler. Pour ce faire le miroir principal de leur télescope doit être percé en son centre d’un petit trou afin qu’y soit placé l’oculaire. Gregory renvoie sur cet oculaire la lumière réfléchie par le miroir principal à l’aide d’un petit miroir concave. Cassegrain de son côté a fait le choix d’un miroir secondaire convexe qui a l’avantage de corriger certaines aberrations du miroir primaire. Quant à Newton, c’est à l’aide d’un petit miroir plan placé à 45° sur l’axe optique du grand miroir qu’il renvoie sur l’oculaire la lumière de l’astre réfléchie par le grand miroir. Dans le cas de la combinaison newtonienne, l’astronome n’observe pas derrière le tube du télescope, mais sur le côté, à l’avant du tube du télescope.
D’un point de vue pratique les lentilles en verre de la lunette de Kepler sont considérablement plus faciles à réaliser que des miroirs primaires concaves en bronze. Qui plus est les lunettes sont bien plus lumineuses que les télescopes à miroir en métal qui, se ternissant rapidement, doivent être repolis avec soin très souvent. Autre différence, la construction de la partie mécanique de l’instrument et l’assemblage des pièces optiques sont bien plus simples à réaliser dans le cas de la lunette : de simples tubes cylindriques télescopiques en carton portent à une extrémité l’objectif et à l’autre l’oculaire. Dans le cas du télescope à miroir, l’alignement du miroir primaire, du miroir secondaire – plan pour Newton, concave pour Gregory ou convexe pour Cassegrain – et de l’oculaire est très délicat à réaliser et, une fois réalisé, il se dérègle facilement.
En fait côté anglais nul opticien ne réussira à construire de télescope modèle Gregory et côté français aucun ne se risquera à construire de télescope modèle Cassegrain. En cette fin du XVIIe siècle, seule restera donc en lice la combinaison optique du plus célèbre des trois inventeurs… qui pour ses propres observations astronomiques fera de préférence usage d’une lunette à réfraction.
Notes
1. Et aux traductions ultérieures de l’arabe en espagnol et en latin effectuées en Occident à partir du XIIe siècle.
2 L’original grec, fondement de la traduction en arabe, a disparu. Subsiste la traduction en latin – incomplète – de cette traduction arabe, elle-même perdue.
3 Gérard Simon. Science Savoirs aux XVIe et XVIIe siècle, Villeneuve d’Ascq, Presses universitaires du Septentrion, p.14, 1996, 225 p.
4 Né à Bassora (Irak) en 965 et mort au Caire vers 1039.
5 Gérard Simon. Optique et perspective : Ptolémée, Alhazen, Alberti. In Peinture et Musique : Penser la vision, penser l’audition. Ed. Catherine Kintzler. Septentrion Presses Universitaires. 19-36, 2002.
Crédits des images
1. Page de couverture «Euclide : L’optique et la catoptrique» : Euclide, Paul Ver Eecke. Fondation Universitaire de Belgique, 1938.
2. Page de couverture «Ptolémée : L’optique» : Claude Ptolémée, Eugène de Sicile, Albert Lejeune. L’optique de Claude Ptolémée dans la version latine d’après l’arabe de l’émir Eugène de Sicile. Louvain, 1956.
3. La vision selon Ptolémée : Gérard Simon. Sciences et savoirs aux XVIe et XVIIe siècles. Presses universitaires du Septentrion, p. 15, 1996.
4. La vision selon Alhazen : Gérard Simon. Sciences et savoirs aux XVIe et XVIIe siècles. Presses universitaires du Septentrion, p. 15, 1996.
5. Formation de l’image sur la rétine : William C. Wees. Light Moving in Time : Studies in the Visual Aesthetics of Avant-Garde Film. Berkeley, University of California Press, 1992.
6. La lunette de Galilée : Henry C. King. The History of the Telescope. Griffin & Company Limited, London, p.36, 1955.
7. La lunette de Kepler : Henry C. King. The History of the Telescope. Griffin & Company Limited, London, p.45, 1955.
8. Page de couverture «Kepler : Dioptrice» : Books.google.com
9. Lunette aérienne de 66m de long : commons.wikipedia.org
10. Télescope de Newton : a) Robert Ball. Great Astronomers. Isbister and Company Limited, p 129, 1895. b) Henry C. King, The History of the Telescope, Dover, p.72, 1979.
11. Télescope de Gregory : Henry C. King, The History of the Telescope, Dover, p. 70, 1979.
12. Télescope de Cassegrain : Henry C. King, The History of the Telescope, Dover, p. 76-77, 1979.
Texte par Françoise Le Guet Tully